Back to Schedule
Kevin H. Knuth
University at Albany (SUNY), Albany NY, USA
Quantity-with-Uncertainty Defines the Physics of Quantum Mechanics and Space Time
(joint work with John Skilling)
Science relies on numeric quantification, which can be traced back to Euclid, Galileo, and Newton.
Here we develop the formalism of numeric quantification in the face of intrinsic uncertainty, since at the
smallest scales it is not possible to be able to perform measurements with arbitrary precision. As a result,
a faithful numeric description must depend on a pair of numbers representing a fusion of quantity and
uncertainty, which is potentially more intimate than the familiar quantity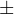 
error bar. We show
that the basic symmetries of combination and partition impose a specific calculus on number
pairs, in keeping with but more subtle than standard scalar arithmetic. We derive complex
arithmetic operating on pairs which we recognize as quantum amplitudes, observable through
modulus-squared probabilities. Not only do we construct the Feynman picture of quantum mechanics,
but we find that these same symmetries also lead to the Pauli matrices which generate spin,
energy and momentum, and beyond that to 
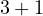-dimensional relativistic spacetime. Not
surprisingly, we find that uncertainty is related to the quantum phase, which is in turn, related
to time. The result is that the physics of quantity-with-uncertainty in conjunction with the
basic symmetries of combination and partition define much of the mathematical formalism of
physics.