Back to Schedule
Masanao Ozawa
Chubu University & Nagoya University, Japan, ozawa@is.nagoya-u.ac.jp
Intersubjectivity of Quantum Measurement II
In a previous workshop, QCQMB 2017, it was shown that if two observers simultaneously
measure the same observable, represented by the same self-adjoint operator, then they always
obtain the same outcome [1]. Thus, the outcome of a measurement of a specific observable at a
specific time is uniquely determined independent of observers to measure. This suggests that the
measurement ascertains the pre-existing value of the measured observable in contrast to the
standard view. Here, we show that if one measures an observable A in an unknown state ψ in a
Hilbert space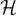 
by an apparatus prepared in a state ξ in another Hilbert space 
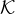with the
meter M by the interaction from time 0 to τ with the time evolution described by a unitary
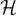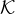operator U on ⊗, then A(0) = A ⊗ I and M(τ) = U†(I ⊗ M)U commute in a common
invariant subspace of 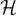⊗ 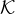including 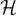⊗ [ξ] and have the joint probability distribution
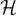P(A(0) = x,M(τ) = y) such that P(A(0) = x,M(τ) = y) = 0 if x ⁄= y in any state in ⊗ [ξ] [2].
Therefore, a measurement reproduces the value of A at the time just before the measurement as the value
of the meter at the time just after the measurement. We argue about reconciliations of apparent
contradictions with the Copenhagen interpretation, the Quantum Baysean interpretation, and the
common interpretation of the Kochen-Specker theorem. We also argue that our result enforces
Bohr’s complementarity view that the measurement arrangement defines the value of the
observable to be measured. We conclude that the pre-existing value of the observable to be
measured can be uniquely defined contextually to be revealed by the measurement independent of
observers, whereas quantum mechanics does not predict the value but only its probability
distribution.
[1] M. Ozawa (2017), Intersubjectivity of Quantum Measurement, QCQMB 2017, Abstracts,
pp. 27–28, available at
(http://www.psych.purdue.edu/~ehtibar/workshop/schedule.html).
[2] M. Ozawa (2019), Intersubjectivity of outcomes of quantum measurements, preprint available at (https://arxiv.org/abs/1911.10893).